The light’s mysteries: refraction

Bonjour guys, 

today I want to tell you about a discovery I came across while I was in Versailles. I went to see a particular painting, entitled “Chat Angora Blanc” by Jean-Jacques Bachelier, which portrays Madame Brillant. According to my family tree, she could be an illustrious ancestor of mine. Here you can see the painting I am referring to and, in fact, it seems to exist a great similarity between us.

As I was telling you, I had gone to visit the places where my ancestor lived and I was struck by the light of the chandeliers in the hall of mirrors: the light was breaking up into many rays of different colors and while this thought was spinning in my head, I went out to admire the garden.

Immersed in my thoughts, I almost didn’t end up immersing myself in the Latona fountain, where I caught a glimpse of a rainbow admist the water droplets from the splashes of the fountain. Back home, I decided to resume my studies on optics, a subject I’m very passionate about, and to write this article, the first of a long and interesting series dedicated to the light and its mysteries.

Here we see the passage of the light beam from material 1 to material 2.

Since the materials have different optical properties, a variation in the angle of the light beam is obtained.

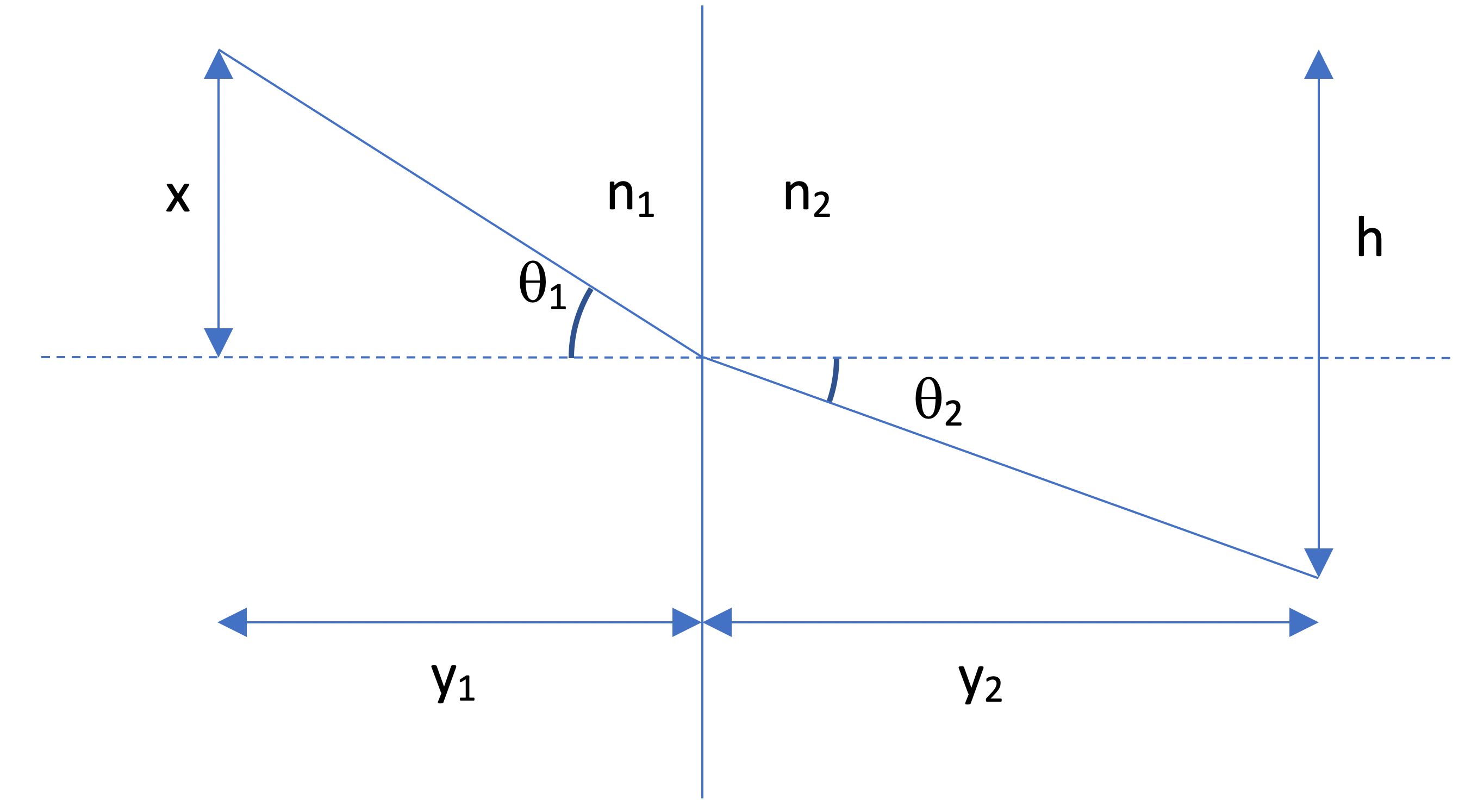
Where: 

• n₁ is the refractive coefficient of the medium 1
• n₂ is the refractive coefficient of the medium 2
• v₁=^c/_n1, speed of light in the medium 1 
• v₂=^c/_n2, speed of light in the medium 2 
• c speed of light in vacuum

 

From Fermat’s principle, we know that light tends to travels the shortest path.

Let’s write the total time it takes for the ray of light to cross the space:

We set the derivative of T to zero, in order to minimize the time it takes for the ray to travel through space:

being by definition: 

and:

Replacing in the previous equation we have: 

We have then:

replacing v₁ and v₂ with the definitions: 

and, finally, simplifying with respect to the speed of light c we have Snell’s law, which defines the angle of refraction due to the passage of light from one material to another:

n₁sin(θ₁)=n₂sin(θ₂)

We’ll therefore have that the new angle of the light will be: 

But this doesn’t explain why light breaks down into different colors: in fact a bit of physics is missing.

The refractive index depends on the frequency, this is the phenomenon that leads the light to break down into different colors, that run through the material at different angles.

Here the formula that explain this:

n=n(λ)

where λ is the wavelength of the electromagnetic radiation of the color considered.

Here I report the intervals of the wavelengths of the different colors: 

• red: ~700–630 nm
• orange: ~630–590 nm 
• yellow: ~ 590–560 nm 
• green: ~ 560–490 nm 
• blue: ~ 490–450 nm 
• purple: ~ 450–400 nm

 
The refractive coefficient can be approximated using the Cauchy equation:

note: in the Cauchy equation, the wavelength is expressed in μm (micro-meters, where 1 μm = 1000 nm). 

For our calculations, I considered a glass with a large refractive index used to build prisms, that is flint glass SF10, with values of the parameters of the Cauchy equation of:

A=1.7280 
B=0.01342

I show below the application of this law for the case of red and blue light.

1. Let’s calculate the refractive index for red light, taking an intermediate wavelength of 660 nm. We’ll have:

2. Let’s calculate the refractive index for blue light, taking an intermediate wavelength of 470 nm. We’ll have:

Now let’s consider the geometry of the prism: 

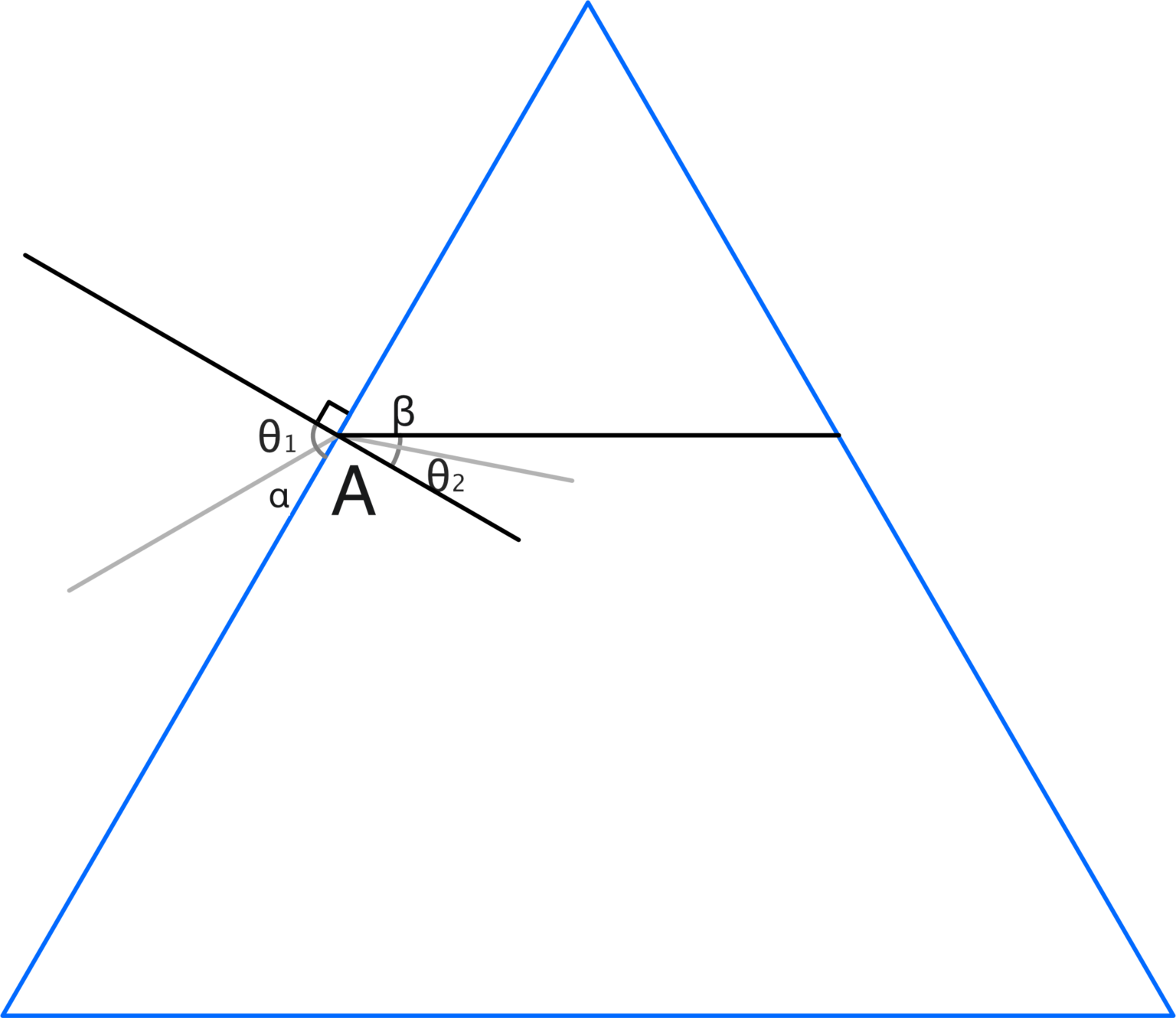
The ray of light hits the prism at point A with an angle α = 30 °; for the geometry of the prism (which is an equilateral triangle), this corresponds to the angle θ₁ = 60 ° (angle with respect to the tangent of the prism surface).

We then calculate θ₂ for the red light:

And for the blue color:

Respect to the horizontal plane in a clockwise direction we have:

β_r = 30-θ_2,r = 0.502°

β_b = 30-θ_2,b = 1.0431°

Now let’s consider the point B where the light beam exits the prism:

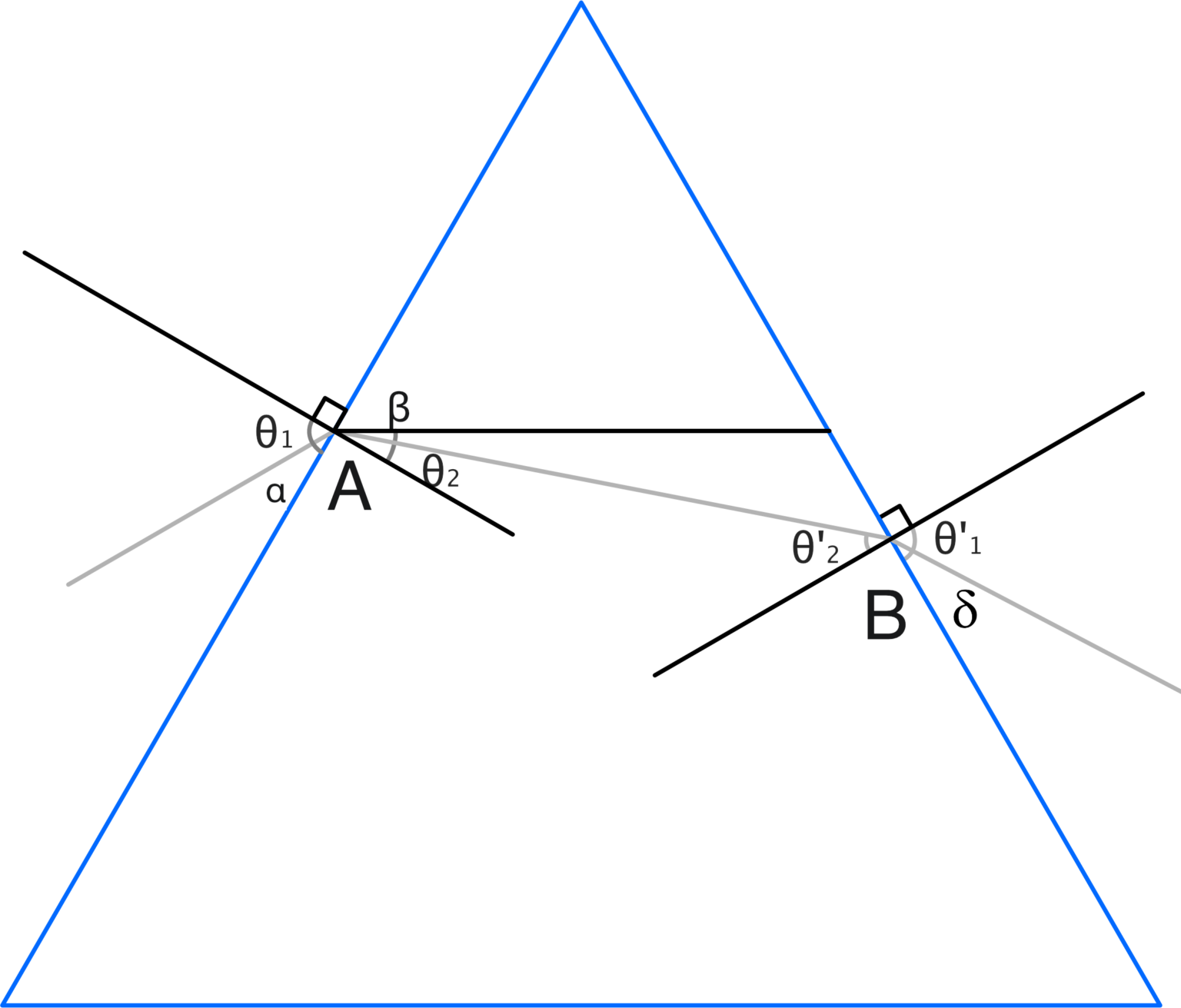
For the geometry of the prism, the angle of incidence θ’₂ is equal to β + 30, so we have:

θ’_2,r = β_r+30 = 30.502°

θ’_2,b = β_b+30 = 31.0431°

Now, let’s calculate the angle θ’₁ of the ray exiting the prism at point B for the red light:

And for the blue color:

Taking all in function of the angle δ we have:

δ_r=90-θ’_2,r= 26.7834°

δ_b=90-θ’_2,b= 22.7164°

We therefore have that the angle between the red light and the blue light is 4.067 ° -> the light is broken down into the various colors that make it up by the prism!

Below we have a fun interactive representation of refraction in a prism, with which you can experience refraction for yourself: